Category: Publications

PLOS One

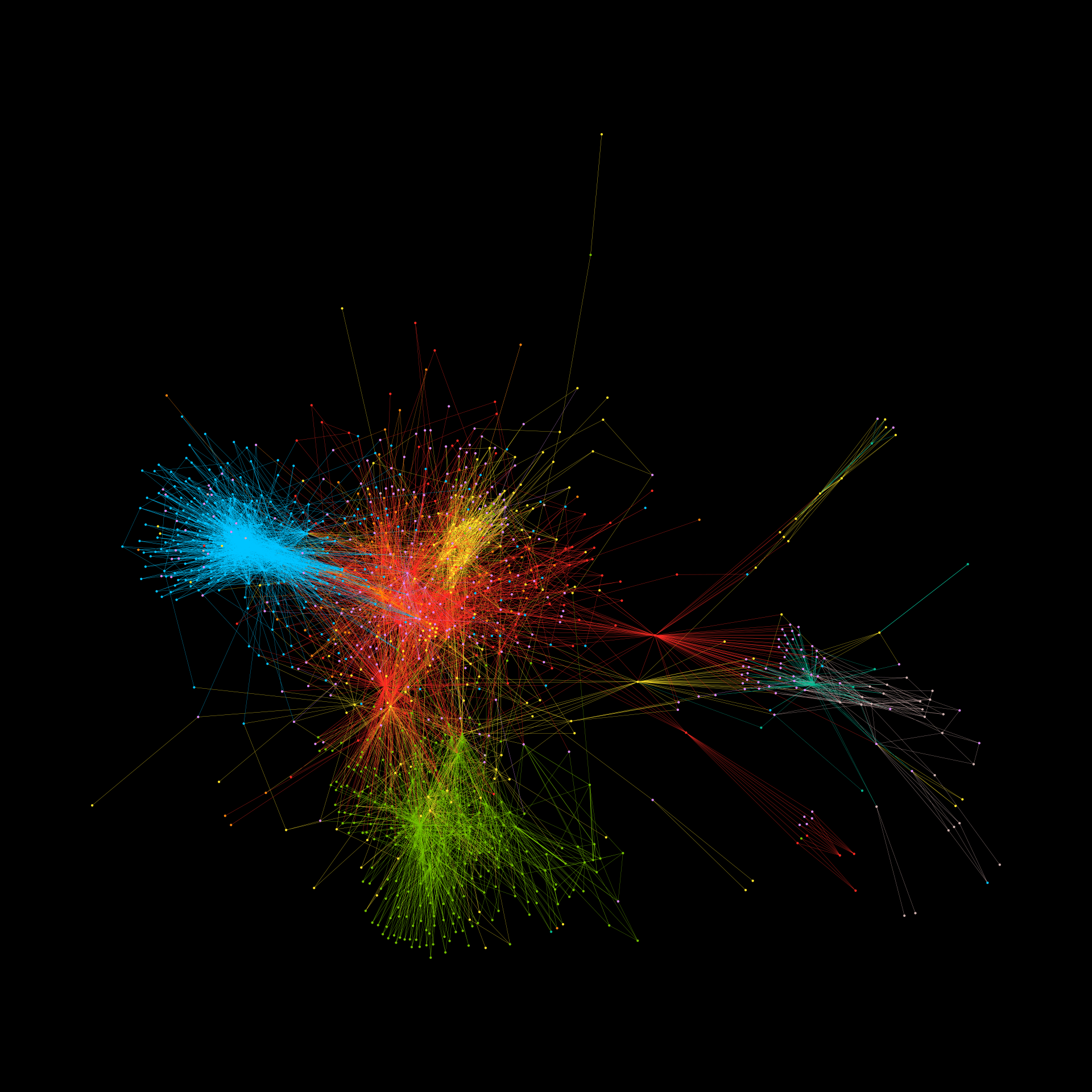
Online hate speech is a critical and worsening problem, with extremists using social media platforms to radicalize recruits and coordinate offline violent events. While much progress has been made in analyzing online hate speech, no study to date has classified multiple types of hate speech across both mainstream and fringe platforms. We conduct a supervised machine learning analysis of 7 types of online hate speech on 6 interconnected online platforms. We find that offline trigger events, such as protests and elections, are often followed by increases in types of online hate speech that bear seemingly little connection to the underlying event. This occurs on both mainstream and fringe platforms, despite moderation efforts, raising new research questions about the relationship between offline events and online speech, as well as implications for online content moderation.

Yonatan Lupu, Richard Sear, Nicolas Velásquez, Rhys Leahy, Nicholas Johnson Restrepo, Beth Goldberg, Neil Johnson

View article >>

Science Advances

Ensuring widespread public exposure to best-science guidance is crucial in any crisis, e.g., coronavirus disease 2019 (COVID-19), monkeypox, abortion misinformation, climate change, and beyond. We show how this battle got lost on Facebook very early during the COVID-19 pandemic and why the mainstream majority, including many parenting communities, had already moved closer to more extreme communities by the time vaccines arrived. Hidden heterogeneities in terms of who was talking and listening to whom explain why Facebook’s own promotion of best-science guidance also appears to have missed key audience segments. A simple mathematical model reproduces the exposure dynamics at the system level. Our findings could be used to tailor guidance at scale while accounting for individual diversity and to help predict tipping point behavior and system-level responses to interventions in future crises.

Lucia Illari, Nicholas J. Restrepo, Neil F. Johnson

View article >>

Intelligent Computing

Online hate speech can precipitate and also follow real-world violence, such as the U.S. Capitol attack on January 6, 2021. However, the current volume of content and the wide variety of extremist narratives raise major challenges for social media companies in terms of tracking and mitigating the activity of hate groups and broader extremist movements. This is further complicated by the fact that hate groups and extremists can leverage multiple platforms in tandem in order to adapt and circumvent content moderation within any given platform (e.g. Facebook). We show how the computational approach of dynamic Latent Dirichlet Allocation (LDA) may be applied to analyze similarities and differences between online content that is shared across social media platforms by extremist communities, including Facebook, Gab, Telegram, and VK between January and April 2021. We also discuss characteristics revealed by unsupervised machine learning about how hate groups leverage sites to organize, recruit, and coordinate within and across such online platforms.

Richard Sear, Nicholas Johnson Restrepo, Yonatan Lupu, Neil F. Johnson

View article >>

Exploring Hate (Brookings)

Rhys Leahy, Nicolas Velásquez, Nicholas Johnson Restrepo, Yonatan Lupu, Beth Goldberg, Neil F. Johnson

View book info >>

Frontiers in Political Science

The current military conflict between Russia and Ukraine is accompanied by disinformation and propaganda within the digital ecosystem of social media platforms and online news sources. One month prior to the conflict’s February 2022 start, a Special Report by the U.S. Department of State had already highlighted concern about the extent to which Kremlin-funded media were feeding the online disinformation and propaganda ecosystem. Here we address a closely related issue: how Russian information sources feed into online extremist communities. Specifically, we present a preliminary study of how the sector of the online ecosystem involving extremist communities interconnects within and across social media platforms, and how it connects into such official information sources. Our focus here is on Russian domains, European Nationalists, and American White Supremacists. Though necessarily very limited in scope, our study goes beyond many existing works that focus on Twitter, by instead considering platforms such as VKontakte, Telegram, and Gab. Our findings can help shed light on the scope and impact of state-sponsored foreign influence operations. Our study also highlights the need to develop a detailed map of the full multi-platform ecosystem in order to better inform discussions aimed at countering violent extremism.

Rhys Leahy, Nicholas Johnson Restrepo, Richard Sear, Neil F. Johnson

View article >>

Advances in Artificial Intelligence and Machine Learning

The natural, physical and social worlds abound with feedback processes that make the challenge of modeling the underlying system an extremely complex one. This paper proposes an end-to-end deep learning approach to modelling such so-called complex systems which addresses two problems: (1) scientific model discovery when we have only incomplete/partial knowledge of system dynamics; (2) integration of graph-structured data into scientific machine learning (SciML) using graph neural networks. It is well known that deep learning (DL) has had remarkable success in leveraging large amounts of unstructured data into downstream tasks such as clustering, classification, and regression. Recently, the development of graph neural networks has extended DL techniques to graph structured data of complex systems. However, DL methods still appear largely disjointed with established scientific knowledge, and the contribution to basic science is not always apparent. This disconnect has spurred the development of physics-informed deep learning, and more generally, the emerging discipline of SciML. Modelling complex systems in the physical, biological, and social sciences within the SciML framework requires further considerations. We argue the need to consider heterogeneous, graph-structured data as well as the effective scale at which we can observe system dynamics. Our proposal would open up a joint approach to the previously distinct fields of graph representation learning and SciML.

Nicholas Gabriel, Neil F. Johnson

View article >>

Proceedings of the 2021 Conference of The Computational Social Science Society of the Americas

The COVID-19 pandemic sparked an online “infodemic” of potentially dangerous misinformation. We use machine learning to quantify COVID-19 content from opponents of establishment health guidance, in particular vaccination. We quantify this content in two different ways: number of topics and evolution of keywords. We find that, even in the early stages of the pandemic, the anti-vaccination community had the infrastructure to more effectively garner support than their pro-vaccination counterparts by exhibiting a broader array of discussion topics. This provided an advantage in terms of attracting new users seeking COVID-19 guidance online. We also find that our machine learning framework can pick up on the adaptive nature of discussions within the anti-vaccination community, tracking distrust of authorities, opposition to lockdown orders, and an interest in early vaccine trials. Our approach is scalable and hence tackles the urgent problem facing social media platforms of having to analyze huge volumes of online health misinformation. With vaccine booster shots being approved and vaccination rates stagnating, such an automated approach is key in understanding how to combat the misinformation that slows the eradication of the pandemic.

Richard Sear, Rhys Leahy, Nicholas Johnson Restrepo, Yonatan Lupu, Neil Johnson

View article >>

Advances in Artificial Intelligence and Machine Learning

Not only can online hate content spread easily between social media platforms, but its focus can also evolve over time. Machine learning and other artificial intelligence (AI) tools could play a key role in helping human moderators understand how such hate topics are evolving online. Latent Dirichlet Allocation (LDA) has been shown to be able to identify hate topics from a corpus of text associated with online communities that promote hate. However, applying LDA to each day’s data is impractical since the inferred topic list from the optimization can change abruptly from day to day, even though the underlying text and hence topics do not typically change this quickly. Hence, LDA is not well suited to capture the way in which hate topics evolve and morph. Here we solve this problem by showing that a dynamic version of LDA can help capture this evolution of topics surrounding online hate. Specifically, we show how standard and dynamical LDA models can be used in conjunction to analyze the topics over time emerging from extremist communities across multiple moderated and unmoderated social media platforms. Our dataset comprises material that we have gathered from hate-related communities on Facebook, Telegram, and Gab during the time period January-April 2021. We demonstrate the ability of dynamic LDA to shed light on how hate groups use different platforms in order to propagate their cause and interests across the online multiverse of social media platforms.

Richard Sear, Rhys Leahy, Nicholas Johnson Restrepo, Yonatan Lupu, Neil F. Johnson

View article >>

IEEE

We reveal hidden social media machinery that has allowed misinformation to thrive among mainstream users, but which is missing from current policy discussions. Specifically, we show how mainstream parenting communities on Facebook have been subject to a powerful, two-pronged misinformation machinery during the pandemic, that has pulled them closer to extreme communities and their misinformation. The first prong involves a strengthening of the bond between mainstream parenting communities and pre-Covid conspiracy theory communities that promote misinformation about climate change, fluoride, chemtrails and 5G. Alternative health communities have acted as the critical conduits. The second prong features an adjacent core of tightly bonded, yet largely under-the-radar, anti-vaccination communities that continually supplied Covid-19 and vaccine misinformation to the mainstream parenting communities. Our findings show why Facebook’s own efforts to post reliable information about vaccines and Covid-19 have not been efficient; why targeting the largest communities does not work; and how this machinery could generate new pieces of misinformation perpetually. We provide a simple yet exactly solvable mathematical theory for the system’s dynamics. It predicts a new strategy for controlling mainstream community tipping points. Our conclusions should be applicable to any social media platform with in-built community features, and open up a new engineering approach to addressing online misinformation and other harms at scale.

Nicholas J. Restrepo, Lucia Illari, Rhys Leahy, Richard Sear, Yonatan Lupu, Neil F. Johnson

View article >>

Advances in Artificial Intelligence and Machine Learning

Any uptick in new misinformation that casts doubt on COVID-19 mitigation strategies, such as vaccine boosters and masks, could reverse society’s recovery from the pandemic both nationally and globally. This study demonstrates how machine learning language models can automatically generate new COVID-19 and vaccine misinformation that appears fresh and realistic (i.e. human-generated) even to subject matter experts. The study uses the latest version of the GPT model that is public and freely available, GPT-2, and inputs publicly available text collected from social media communities that are known for their high levels of health misinformation. The same team of subject matter experts that classified the original social media data used as input, are then asked to categorize the GPT-2 output without knowing about its automated origin. None of them successfully identified all the synthetic text strings as being a product of the machine model. This presents a clear warning for social media platforms: an unlimited volume of fresh and seemingly human-produced misinformation can be created perpetually on social media using current, off-the-shelf machine learning algorithms that run continually. We then offer a solution: a statistical approach that detects differences in the dynamics of this output as compared to typical human behavior.

Richard Sear, Rhys Leahy, Nicholas Johnson Restrepo, Yonatan Lupu, Neil F. Johnson

View article >>